When I started to work on the video tool that measures vertical jump, I had to dust off my old textbooks to learn about the relationship between hang time and jump height. And to my surprise, it turned out that the vertical jump is a great (and interesting!) example of the laws of physics at work. You can really learn about the relationship between velocity, acceleration, forces and hang time. Definitely more interesting than the average example of your physics textbook!
In this article, I am going to look at the five phases of the vertical jump and show you how physics work during each of them. This will be accompanied by charts and interactive calculators, and in the end, we are going to answer some fun questions like: "How high would Micheal Jordan jump on the Moon?".
Let's start!
A great way to look at the physics of the vertical jump is to look at the forces that occur during each phase:
Ground reaction forces during a vertical jump
Ground reaction forces are the forces that the ground exerts on a jumper during the course of a vertical jump.
You're maybe asking yourself: "Isn't it the other way around? Isn't the athlete exerting forces on the ground instead of the ground on the athlete?"
You are not wrong! In fact, both forces occur during a vertical jump. This phenomenon is explained in the 3rd Newton Law:
So if an athlete is exerting forces on the ground, then the ground is always exerting the same force, in the opposite direction on the athlete.
Force Plate Analysis
Sports scientist are able to measure these ground reaction forces with a technology called force plates. These plates record the exact forces occurring during a vertical jump (or any other movement) and allow you to see how quickly athletes can produce forces, how large these forces are, and to expose potential imbalances between the left and right leg.
For an example of a force plate analysis check out this Youtube video:
Analyzing the forces of a vertical jump
In the following paragraphs, we want to look at the relations between forces, acceleration, speed, and height of a vertical jump. For that, we are going to use this example of a force plate analysis. It is a little simplified. as in reality the force curve wouldn't be as smooth, but it will work just fine as an example:
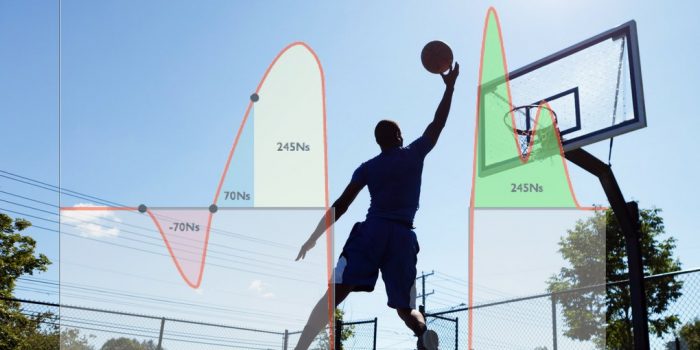
Graph 1: Ground reaction forces during vertical jump:
Phase 1: Before the Jump
Before the jump, the analysis shows a flat line at a force of 981 Newton. The athlete is not moving at that time, so where are these forces coming from?
Of course, this is gravity which is pulling the athlete toward the ground. This force is explained in this formula:
Where is the mass of the athlete and
is the acceleration of earth's gravity.
F is the amount of force the athlete has to exert at any moment just to neutralize the forces of gravity.
We know that on earth, therefore:
So, before the athlete starts any motion, the force plate basically acts as a simple weighing scale, showing the amount of force that gravity exerts on the athlete.
Phase 2: Descending into the Jump
1. Accelerating the downward movement:
During this phase, the athlete bends his knees, swings his arms and prepares the jump by lowering the center of gravity. The force plate is registering forces lower than the 981N needed to resist gravity, which means the athlete is accelerating a downward movement.
The acting forces at this time can be described as follows:
One measure that is interesting to sports scientist is how fast the athlete is moving downwards before the jump. But are we able to calculate that from the recorded forces of the analysis?
We know that:
Because F is not constant but a function of time, and :
where is the difference between the registered ground reaction forces and gravity.
This integral can be numerically calculated from the data obtained by the force plate analysis. The downward impulse generated by the jumper is shown in the graph as the red area below the line representing gravity:
Graph 2: Forces during Phase 2
Let's assume a numerical estimation finds the integral (impulse) to be -70 Ns. We can then conclude that:
Therefore, the athlete reaches the highest velocity of 0.7 meters/second during the downward movement preceding the jump.
2. Decelerating the downward movement
So far we only looked at the first part of the countermovement, where the athlete is accelerating his downward movement. This part of the movement can be easily identified on the force-time diagram as the part where ground reaction forces are below the expected forces due to gravity.
The second part of the countermovement is less obvious. The athlete has to decelerate the downward movement to reach a short moment of pause at the deepest position of the jump.
Can we find this moment in the graph of the force plate analysis?
We have seen that during the first part of phase two we accumulated a downward impulse of 70Ns which resulted in a velocity of 0.7 m/s
We are now looking for an equally big impulse in the opposite direction. This impulse can be described as:
As and
are known, the numerical algorithm of the force plate analysis is now looking for
so that the impulse equals 70Ns.
To better picture it, imagine looking for a so that the pink and blue areas are exactly the same size:
Graph 3: Forces during Deceleration of Phase 2
Phase 3: Upward Motion before takeoff
This phase begins with the athlete at the bottom of the jump, just as he begins exploding upwards towards the takeoff. The force-time graph shows that the athlete reaches peak forces shortly after reaching the lowest point of the jump. He then further accelerates until his feet leave the ground and there are no more ground reaction forces measurable.
If you want to assess the velocity during takeoff we can use the same technique as during phase 2:
This integral can be pictured as the yellow area (subtracting the small brown area right before the takeoff) in the following force-time graph:
Graph 4: Forces during Upward Motion
The numerical algorithm of the force plate analysis calculates an impulse of 245Ns, therefore we can determine the initial vertical velocity during takeoff as:
Phase 4: The Flight
During this phase, the athlete can't impact the velocity of his center of gravity any further. The height of the jump has been predetermined by the build up of speed before and during takeoff. The only force that is now acting upon the athlete is the gravity that is pulling the jumper back down.
If the athlete can't do anything at this point to increase his vertical jump, can we then determine the jump height using the recorded ground reaction forces during phases 1-3?
We do know so far that the initial velocity and that the gravity of earth has an acceleration of
We also know that during the peak of the jump, vertical velocity has to be zero as otherwise, the athlete would still gain height, which would also mean that he hasn't reached the peak of the jump yet.
If we know initial velocity and earth's gravity, we can calculate the velocity during every moment of the jump like this:
Therefore, we can calculate the time it takes the jumper to reach the peak of the jump as follows:
So now that we know the velocity during every moment of the jump, and the time of the peak of the jump 0.25s we can calculate the jump height as the integral of velocity over the time it takes to reach the peak of the jump:
So, we end up with a pretty simple formula that allows us to calculate the vertical jump height if we know the initial velocity. In our specific case we get:
This interactive graph shows the relationship between impulse, mass of the jumper, initial velocity and jump height:
Calculate Vertical Jump Height based on impulse, velocity and weight:
If you are a sports scientist and you have access to a force plate then this is great! But are there easier ways to calculate vertical jump height using physics?
Calculating vertical jump height from hang time
Let's assume we have no idea about the forces during takeoff or the initial velocity of the jumper. We know, however, the time the jumper was in the air (hang time). This is not a very unrealistic expectation as you can measure hang time using high frame rate cameras or even modern cell phones pretty easily.
In our example we have measured a hang time of .
We already established that we can calculate vertical jump height as a product of initial velocity:
So, now we just need to find the initial velocity for a vertical jump that takes 0.5s!
If a jumper jumps 1m high it also means he has to fall 1m after he reaches the peak of the jump. And as velocity is a linear function we can show that the jumper reaches the peak of the jump always exactly in the middle of a jump. Therefore:
So, if we want to know how high someone with a hang time of 0.5s jumped, we can just calculate the distance a free falling object travels in 0.25s! In general:
In our specific case with a hang time of 0.5s we get:
This formula is at the heart of the vertical jump measurement app I have created. If you have video of your jump you can load it in the browser, tag the takeoff and landing, and the app will tell you your vertical jump height. You can also check out the iPhone version on the App store here.
Phase 5: Landing
During the takeoff an athlete generates forces that ultimately result in a vertical velocity high enough to leave the ground. We have shown before, that this vertical velocity reaches 0 at the peak of the jump, and it is easy to show that the velocity is exactly the same during landing as it was during takeoff (but directed in the opposite direction).
If the athlete wants to stop the downward movement and come to a standstill he has to exert enough forces to cancel out the impulse of the vertical speed of the landing:
This impulse can be pictured as the green area in the following graph:
Graph 5: Forces during Landing
In our example, the athlete accelerated from a velocity to
, during the landing he has to accelerate from a velocity of
to a speed of
.
As the change in speed is the same in both cases, the Impulse has to be the same too. This can be seen in the graph as both the yellow and the green area result in 245Ns.
The athlete is now back in a standstill and the 5 phases of the vertical jump are complete!
Questions answered by physics
Now that we have learned the relationship between physics and the vertical jump. Let's answer some fun questions! If you want to try your knowledge and answer them yourself, you can check out the equation collection or the interactive calculator at the end of this post.
How high would Micheal Jordan jump on the Moon?
During his prime, Micheal Jordan had a vertical of at least 110cm. So far we have taken the acceleration of earth for granted. But what happens if you look at the gravity of the moon?
Answer:
If we assume that MJ is able to generate the same impulse during takeoff on Moon as on Earth then his initial vertical velocity would be unchanged. However, velocity during the time of flight would change drastically, as it is no longer decelerated by the gravity of earth (
) but by the gravity of Moon (
).
If we want to get the precise height of the jump we just have to look at this formula for vertical jump height:
Gravity on Moon is about 1/6th of the gravity on Earth, therefore MJ would be able to jump six times as high (665cm)!
Do Jumpers really stop in the air?
Just get the new Air Jordan basketball shoes and you'll be able to hang in the air forever, right? Jokes, aside, do jumpers really stop in the air?
Answer:
The height of a jumper during each moment of the jump is described by this formula:
In this interactive graph shows the plane of flight:
We can see that a jumper spends 10% of his hang time in the top 1% (or 50% of his hangtime in the top 25%). In general:
So the answer is no, the jumper is not really hanging in the air, but it appears this way because the athlete spends a disproportional amount of the hang time at the peak of the jump.
If you lose weight, will you be able to jump higher?
Assuming you lose weight but keep all the strength and power, will you be able to jump higher?
Answer:
If an athlete loses 10% of his body weight but remains able to generate the same forces during takeoff, then he significantly improves his takeoff velocity!
My first idea about how to calculate the change in jump height, was to assume that the impulse stays the same if the jumper loses weight but the forces remain the same. But this way I got results that just didn't seem right...
It took me a while but I finally recognized why! Look at the definition of the impulse:
stays the same, but for a lighter athlete, these same forces result in a larger acceleration which in turns makes the takeoff much quicker. This means, that the time during which the jumper can exert forces becomes less and therefore the impulse decreases as well.
A better way to look at this problem is to assume that the potential energy of the body remains constant:
Let's take a look at the formula for the gravitational potential energy that the jumper possesses at the peak of the jump:
If we asume to be constant then we get for the new jump height:
So if you lose 10% bodyweight while everything else stays the same, you would improve your vertical jump by 11.1% ! If is the weight loss in %, then in general:
Interactive Vertical Jump Calculator
Collection of equations
where is intitial velocity and
is the acceleration of gravity
where is intitial velocity and
is the acceleration of gravity
where is the duration of time between takeoff and landing and a is the acceleration of gravity
where
Where I is the area under the force-time curve (minus gravity forces) from the start of the jumping motion until the takeoff.
References
Vertical Jump Calculator: https://www.thehoopsgeek.com/measurement-app
What's my Vertical iOS App https://itunes.apple.com/us/app/whats-my-vertical-vertical-jump-analyzer/id1237413241?mt=8
Analysis of Standing Vertical Jump - Nick Linthorne
https://www.brunel.ac.uk/~spstnpl/Publications/VerticalJump(Linthorne).pdf

Founder of thehoopsgeek.com. A passionate basketball enthusiast and coding geek, Andy combines a love for sports with technology.







Where are the graphs?
They should be there! Check if you have turned off Javascript in your browser, you need to enable Javascript to see the interactive charts.
There’s a bit more to “hanging in the air” than a natural trajectory having the lowest velocity near the peak.
Strong athletes will, probably subconsciously, pull their legs up near the peak of their jump. This pulls their upper bodies down (Newton’s second law), which creates the illusion that their trajectory is flatter at the peak, even though their center of mass is still following that parabolic trajectory.
Hi Joel, thanks for the comment!
While you are right that pulling up the legs would push down the body of the athlete, I feel like basketball players intuitively do the exact opposite. For example, when players try to block shots their bodies are usually extended all the way to the toes
Great article, thanks!
Is peak velocity in the jump just before we leave the ground?
Correct! After that we can no longer accelerate and gravity will deceleratevus.